1B 빈번한 단어 문제

개요

앞선 문제에서는 입력된 pattern이 얼마나 등장하는지, 즉, Pattern → count 였다면, 이번에는 pattern에 대한 조건을 다루어 볼 수 있다. 즉, 원하는 길이의 Pattern 중 가장 많이 등장하는 k-mer를 찾을 수 있다.

앞선 목표: Pattern → count

이번 목표: k → Pattern

Brute-Force를 통해 알고리즘을 수행하면, 이전에 구현한 PatternCount를 이용해, 다음과 같은 아이디어를 이용할 수 있다.

1. 문자열의 모든 문자 하나하나를 시작점으로 하는 k-mer pattern 에 대해
2. 주어진 입력 문자 text를 PatternCount로 count

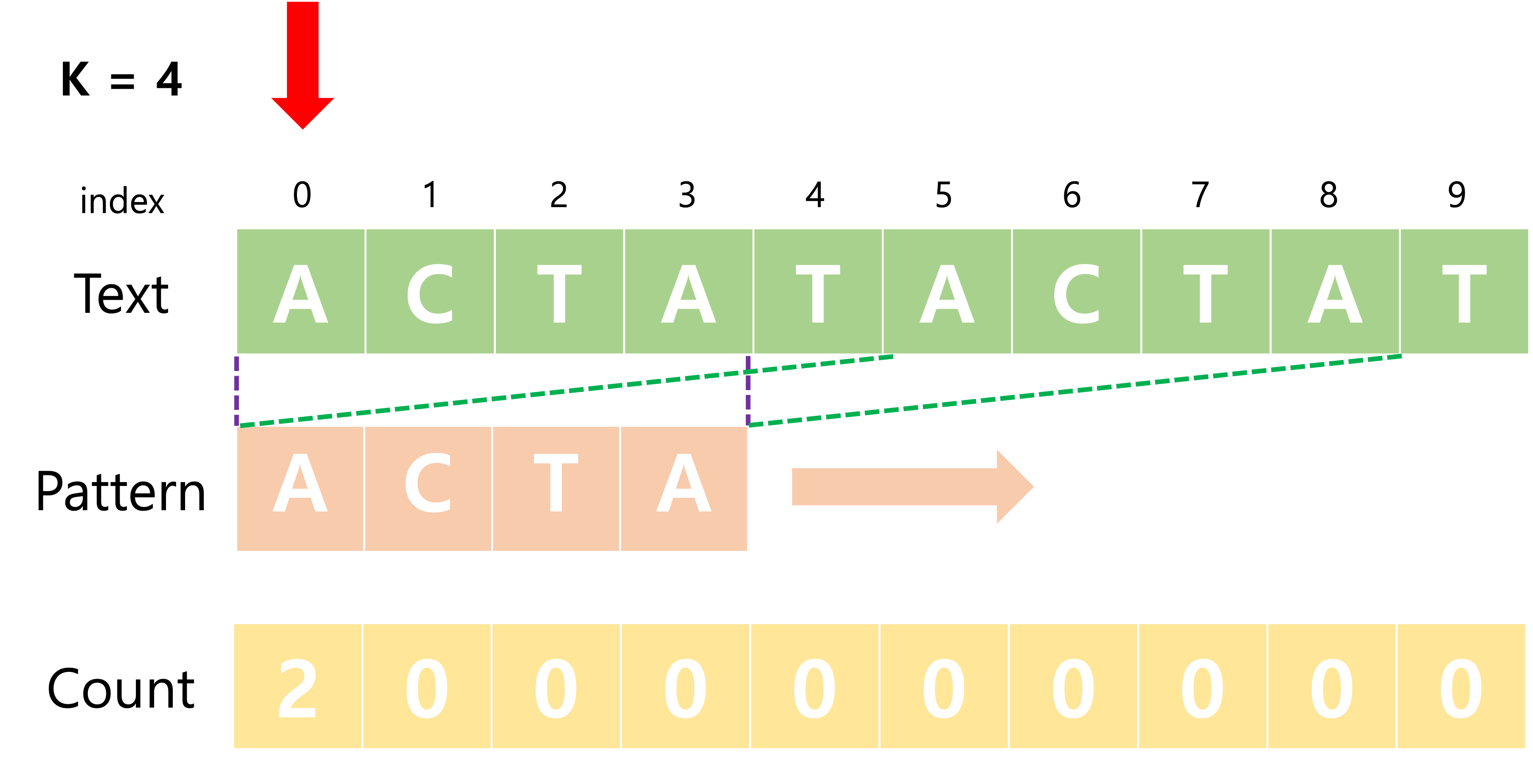
Fig 1. index가 0일 때 pattern count

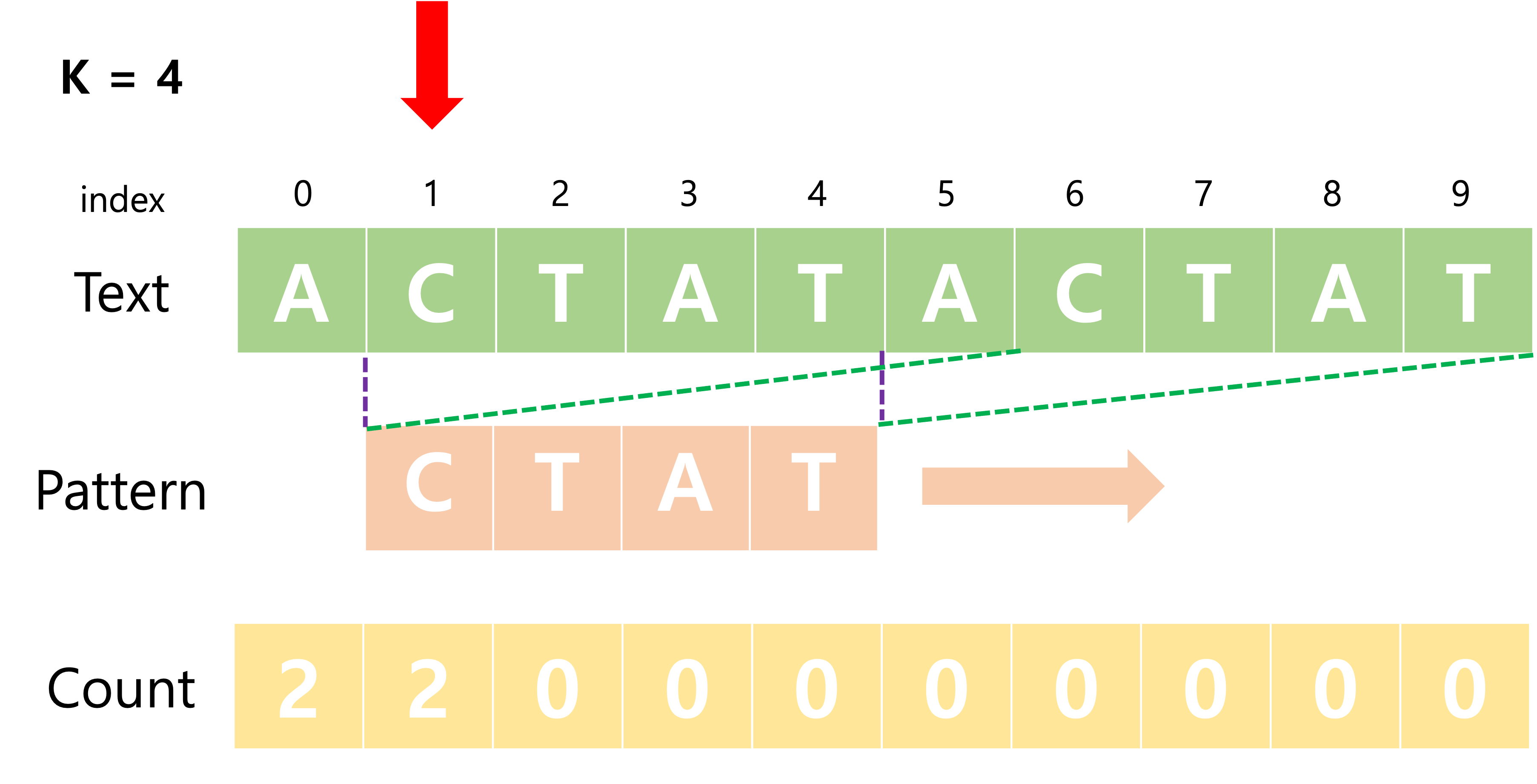
Fig 2. index가 1일 때 pattern count

Problem

• Input: 전체 문자열 Text, Text에서 찾으려는 문자열 Pattern의 길이 k
• Output: 가장 빈번하게 등장하는 k-mer
• function: k $\to$ Pattern

Pseudo-code

FrequentWords(Text, k)
    FrequentPatterns <-- empty set
    count = []
    for i <- 0 to |Text| - k
       	Pattern = Text(i, i + k)
        count[i] = PatternCount(Text, Pattern)
    find index of max count
    return Text(index, index + k)
    

Evaluation

Time Complexity

입력 크기: $\left\vert Text \right\vert = n, \left\vert Pattern \right\vert=k$​

$\text{Constraints: n ≥ k}$

• line[2] ~ line[3: 대입연산 $\to O(1)$​
• line[4]: k-mer 형성이 가능한 모든 문자 순회 반복문 $\to O(n-k)$
• line[5]: 문자열 슬라이싱 $\to O(1)$
• line[6]: PatternCount $\to O(nk)$
• line[7]: find index of max count $\to O(n\log{n}) ~ O(n^2)$
  • 최대값을 찾는 과정은 정렬을 수행¹

Total Time Complexity: $O(1) + O(n-k) \times (O(1) + O(nk)) + O(n^2) \approxeq O(n^2k)$

Implementation

# 주어진 text에서 특정 words의 빈도수를 계산하여 빈도수가 가장 높은 k-mer를 기록하고 반환하는 함수
def FrequentWords(text, k):
    
    # 입력된 text와 같은 크기로 등장 빈도수를 동일한 인덱스에 저장하는 리스트 선언
    count = [0 for i in range(len(text))]

    # 출력할 최대 빈도수의 pattern을 저장할 set 선언 - uniqueness로 중복 값을 저장하지 않음
    FrequentPattern = set()
    
    # i-th value가 가지는 k-mer의 빈도 수를 count라는 배열에 저장
    for i in range(len(text) - k + 1):
        pattern = text[i:i+k]
        count[i] = PatternCount(text, pattern)

    # count의 원소가 maxCount인 pattern을 FrequentPattern으로 저장
    maxCount = max(count)
    for i in range(len(text) - k):
        if count[i] == maxCount:
            FrequentPattern.add(text[i:i+k])

    return FrequentPattern

• Rosalind
• Code in Github

Discussion Points

Summary

1. 주어진 임의의 서열에서 가장 빈번한 pattern이 무엇인지 확인할 수 있다.

Implementation Strategy

1. 이전에 구현한 PatternCount를 통해 가능한 모든 k-mer 조합이 전체 text에서 등장하는 횟수를 모두 배열(count)에 기록
2. 기록된 배열 중 가장 큰 count를 가진 pattern을 다시 반환함
3. 가장 많이 등장하는 pattern이 어떤 pattern인지 확인할 수 있었다.

implications

• 이전 장과 서론의 문제 해결 아이디어를 더불어 생각해보면, k → Pattern → count로 어떤 k-mer가 가장 많이 등장하는지도 확인할 수 있을 것이다.
• 이러한 접근은 아무 정보도 주어지지 않은 상태에서 어떤 임의의 반복 서열이 가장 많은 count를 가지는지 확인할 수 있는 단서로 활용할 수 있을지도 모른다.

다음 문제에서는, 이번에 찾은 다양한 Pattern들과 연관된 상보적인 서열 의 등장 횟수를 고려하여, 빈번한 pattern이 우연이 아닌 상관관계/타당성을 가진다고 말할 수 있는지 알아보도록 하겠다.

Reference

1. Compeu, P., Pevzner, P. (2018). Bioinformatics Algorithms 3/e. 에이콘 출판사
2. Craig, N., Cohen-Fix, O., Green, R., Greider, C., Storz, G., & Wolberger, C. (2010). Molecular biology: Principles of genome function. Oxford University Press.