1E 군집 찾기 문제

개요

이전 장의 결과로부터 우리가 찾은 frequent pattern ATGATCAAG는 그 위치가 군집을 이룬다는 발견 을 했다. 이 결과에 이어, 이번 장에서는 pattern이 정말 군집을 이루는지 정량적으로 분석하도록 하였다.

군집을 이룬다는 것을 어떻게 정의할 수 있을까? 직관적으로, 특정 문자열 pattern이 전체 유전체에서 등장하는 “밀도”가 높을 때 군집을 형성한다고 생각할 수 있다. 일반적으로 밀도는 단위 부피 당 질량을 의미하며, 다음과 같이 정의된다.

$\rho = w / V$
$(where\,\rho:\,density,\,w:\,weight,\,V:\,volume )$

이러한 접근에 근거하여, 군집을 이루는 기준을 다음과 같이 정의할 수 있다.

전체 문자열 중 임의의 영역 L에서 pattern의 등장하는 빈도 수

이번 장에서는 특히 등장하는 빈도수가 어느 정도 이상인 pattern을 찾기 위해, t라는 parameter를 추가하였다. 이는 곧 등장 빈도수가 t번 이상인 pattern만 확인한다는 것을 의미한다. 또, pattern의 길이를 k-mer로 고정하였다.

이를 정리하자면, 다음의 그림과 같이 전체 문자열 Genome 내에서 L만큼의 영역의 substring을 가져오고, 이 substring 내에서 등장하는 모든 k-mer의 빈도를 센 뒤, 빈도가 t번보다 많이 나오면 이를 clump를 이루는 pattern으로 반환한다.

$\text{Find all K such that f(K, S) ≥ t for any S = genome[i:i+L],}$
$\text{where i≥0 and i+L ≤ length of genome}$
$ \text{K for k-mer patterns,}\; \text{f for function to find clumps}$

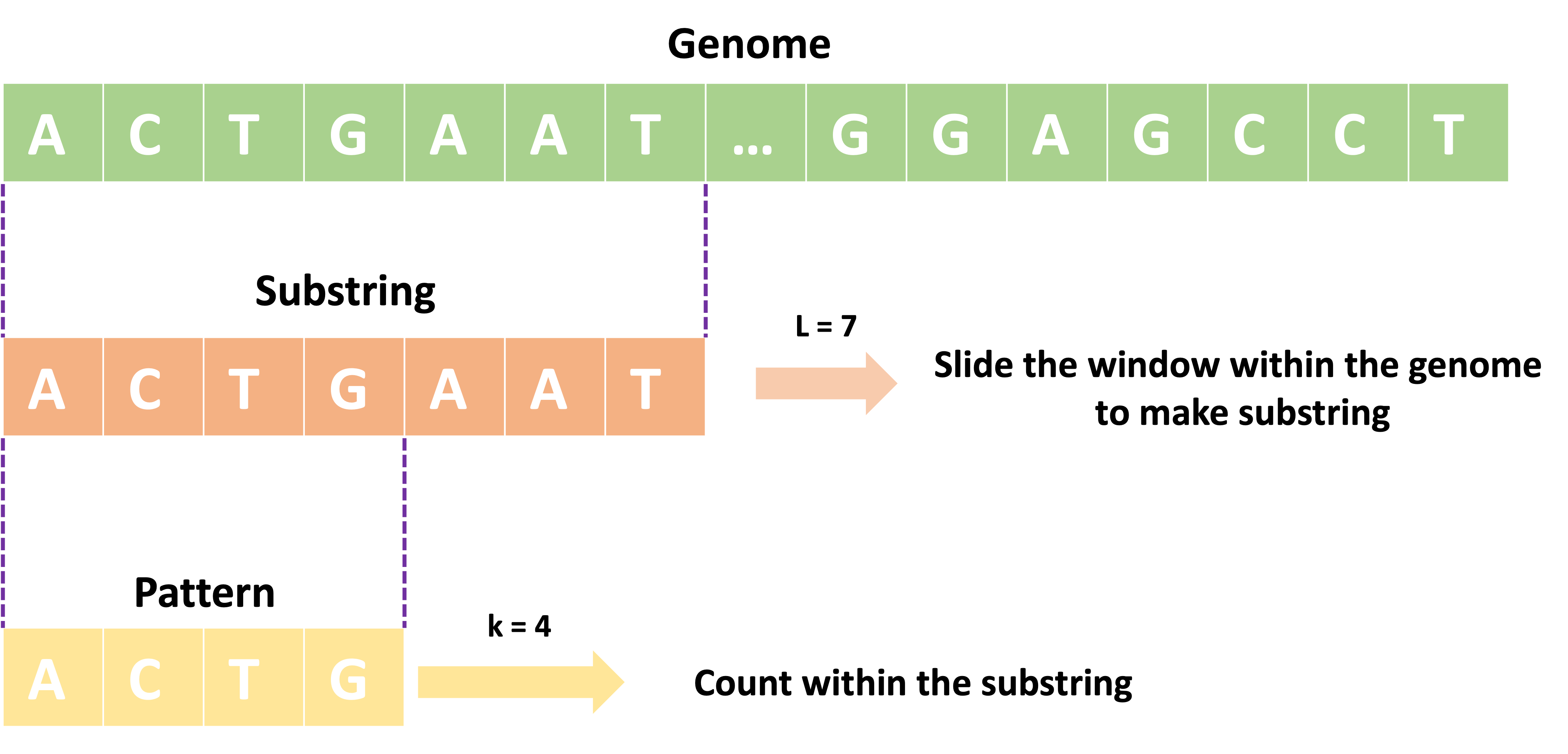
Idea to calculate and find the clumps in genome

Problem

Input: 문자열 유전체 Text, 정수 k, L, t
Output: Text의 L 길이의 임의의 영역에서 t번 이상의 빈도로 등장하는 k-mer

Pseudo-code

findClummps(genome, k, L, t)
    clumpPatterns <-- empty set
    
    for i <-- 0 to |genome|- L + 1
        substring = genome[i:i+L]
        
        for j <-- 0 to |substring| - k + 1
            pattern = substring[j:j+k]
            count the occurrence of the pattern in the substring
        
        if count >= t:
            add pattern to clumpPatterns
        
        return clumpPatterns

Evaluation

Time Complexity

위 알고리즘의 경우 genome의 모든 문자열을 시작점으로 하여 모든 경우의 수를 순회한다. 이는 correct solution을 보장하지만, 어느정도 중복되는 부분이 있을 수 있다. 이에 대한 간략한 논의는 Discussion에서 해보도록 한다.

입력 크기: $\left\vert genome \right\vert = n, k, L, t$

$\text{Constraints: n ≥ L ≥ k,\,t}$

line[2]: 변수 초기화 → $O(1)$
line[4] ~ line[5]: 유전체에서 매 iteration마다 유전체의 모든 문자열에 대해 L 길이만큼 substring으로 slicing 해옴 → $O(n - L + 1) \approxeq O(n)$
line[7] ~ line[8]: substring의 모든 문자열에서 k-mer를 pattern으로 slicing 해옴 → $O(L-k+1)\approxeq O(L)$
line[9]: 이전에 구현한 PatternCount를 사용할 수 있음 → $O(Lk)$ ¹
line[11] ~ line[14]: 비교연산, set.add()², 반환 → $O(1)$

Total Time Complexity: $O(1) + O(n) \times O(L) \times O(Lk) + O(1) \approxeq O(L^2 \cdot n \cdot k)$

Implementation

# 주어진 유전체 문자열에서 크기가 L인 윈도우만큼을 순회하여 각 윈도우에서 t만큼의 빈도로 등장하는 k-mer를 배열로 출력
def myFindClumps(genome, k, L, t):
    
    # Clumps에 해당하는 k-mer를 저장할 리스트 선언
    ClumpPattern = set()

    # genome에서 길이가 L인 substr을 가져오는 반복문
    for window in range(len(genome)-L+1):
        
        # 주어진 windoe 범위 내에 있는 substr(length: L)을 slicing
        substr = genome[window:window+L]

        # L-substr에서 모든 문자열에 대한 순회 시작
        for i in range(L-k+1):
        
            # 각 시작점에서 형성되는 k-mer를 pattern으로 설정
            pattern = substr[i:i+k]
            
            # 현재 window의 substr에서 pattern의 등장 횟수를 저장
            count = PatternCount(substr, pattern)
            
            # 만약 기록된 pattern의 빈도가 t와 같다면 ClumpPattern 에 저장
            if count >= t: 
                ClumpPattern.add(pattern)
            
    return ClumpPattern

Discussion Points

Summary

단지 빈번한 단어를 찾는 것은 “어디에서 얼마나 등장하는지” 에 대한 위치 정보를 포함하지 못함
이는 clump라는 군집을 정의함으로써 등장하는 빈도를 마치 밀도처럼 계산할 수 있음

Implementation Strategy

genome에서 L만큼 substring을 slicing
substring에서 k만큼 pattern을 slicing
pattern의 substring에서의 등장 빈도 확인
t 이상이면 clumpPattern에 저장

Implications

이번에 구현한 알고리즘은 정답을 보장하지만 효율적이지는 못함
substring을 가져올 때 현재 인덱스의 L과 다음 인덱스의 L에서 L-2개의 문자열이 중복되기 때문 (아래 그림 참조)
이에 대한 논의는 추후 충전소 - 빈도 배열을 통해 해결할 수 있다.
한편, PatternCount 대신 window loop에 FrequentWords를 사용함으로써 더 간단하게 구현할 수 있다.³

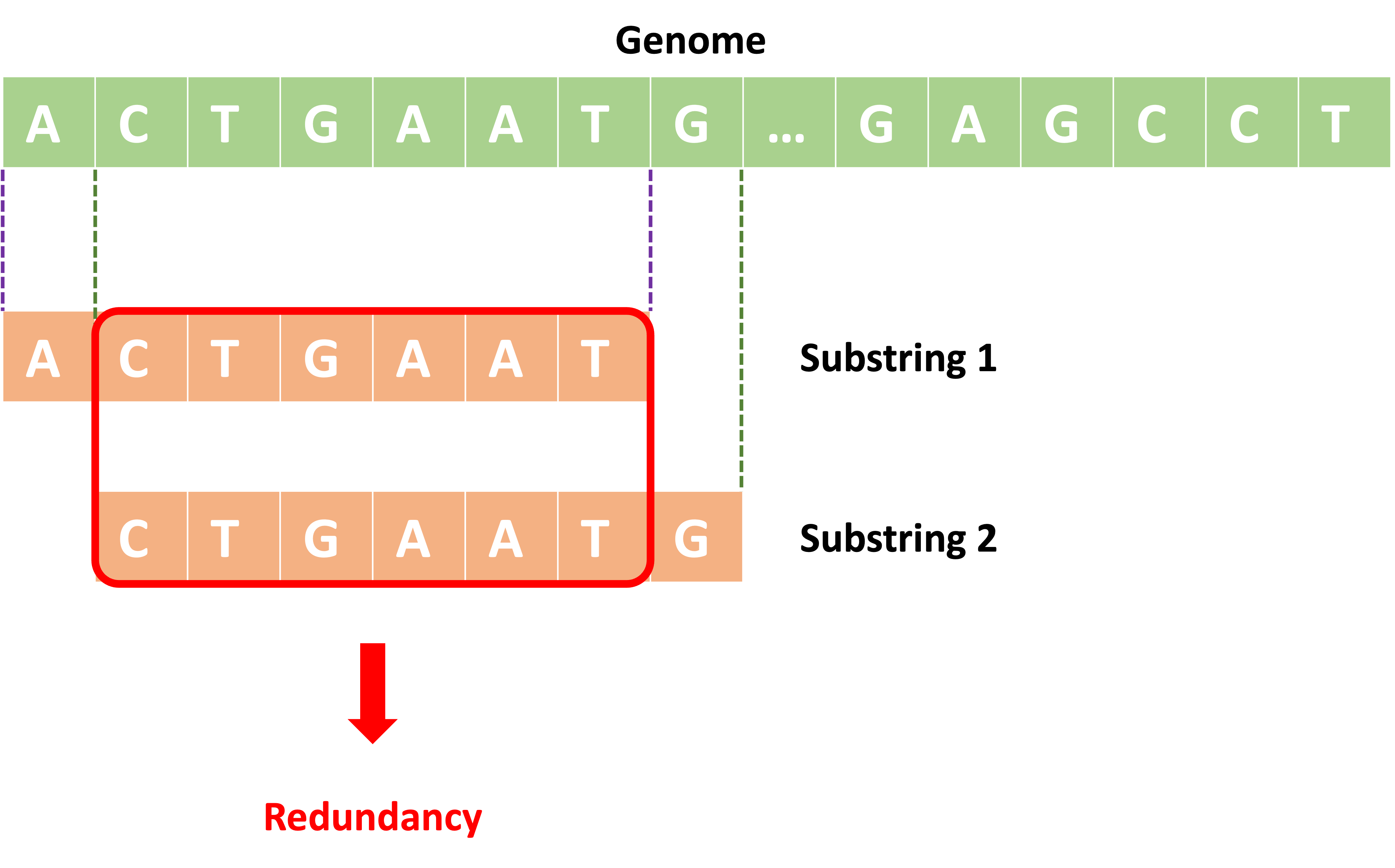
Redundancy in Brute-Force Algorithm to find clumps

Reference

Compeu, P., Pevzner, P. (2018). Bioinformatics Algorithms 3/e. 에이콘 출판사

이전 PatternCount(text, pattern)에서 입력 text가 substring이 되므로, O(Lk)가 됨 ↩
python에서 집합은 hash 구조로 이루어져 있으며, 평균적으로 O(1), 최악의 경우 O(n)이지만 내부 최적화로 O(1)로 간주 ↩
이 경우 역시도 시간복잡도는 $O(L^2 \cdot n \cdot k)$ 로 동일하다 ↩

PREVIOUS1D 패턴 일치 문제